로지스틱 회귀(logistic regression)
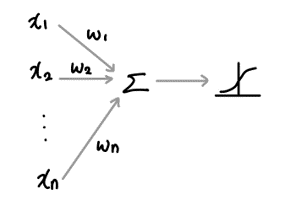
선형 회귀를 입력으로 받아 특정 레이블로 분류하는 모델
시그모이드 출력값은 0~1까지의 값을 가지므로 확률로 사용될 수 있음
- 0.5 이상의 경우 참
- 0.5 이하의 경우 거짓
로지스틱 회귀 학습
경사하강법으로 최적의 w를 찾고 비용함수로 크로스 엔트로피(cross entropy) 사용
(선형 회귀의 경우 MSE 사용)
비선형성을 지니고 있는 시그모이드 함수 때문
선형 vs 비선형
y=w_1 x+w_2 x^2+w_3 x^3+w_4 x^4는 y=w_1 x_1+w_2 x_2+w_3 x_3+w_4 x_4라고 표현이 가능하므로 선형함수
로지스틱 회귀=1/(1+e^(-y))는 로지스틱 회귀=1/(1+e^(-(w_1 x_1+w_2 x_2+w_3 x_3+w_4 x_4)))는 선형 결합이 아니므로 비선형함수
선형함수는 MSE가 convex function이므로 경사하강법으로 최저의 에러를 찾을 수 있음
로지스틱 회귀의 MSE는 선형회귀+시그모이드 함수의 형태이므로 한 개 이상의 로컬 미니멈을 가질 수 있음
→ 글로벌 미니멈의 w가 아닌 로컬 미니멈의 w로 모델 학습이 마무리될 수 있음
→ MSE는 로지스틱 회귀의 적합한 비용 함수가 아님
크로스 엔트로피
서로 다른 두 확률 분포의 차이
→ 로지스틱 회귀 관점에서 모델의 예측값의 확률과 실제값 확률의 차이
크로스 엔트로피=-∑p(x)logq(x)
p(x): 실제 데이터의 분포
q(x): 모델의 예측의 분포
- 실제값과예측값이 완전히 다르면 무한대의 값이 나옴
- 실제값과예측값이 완전히 동일하면 0의 값이 나옴
다중분류 로지스틱 회귀 by 소프트맥스

단일 입력 로지스틱 회귀
다중 입력 로지스틱 회귀 https://github.com/ornni/ML_algorithm/blob/main/logistic_regression/multi_input_logistic_regression_code.md
소프트맥스 다중분류 로지스틱 회귀
'AI&ML > ML algorithms' 카테고리의 다른 글
| 앙상블 (0) | 2022.08.26 |
|---|---|
| Naive Bayes (0) | 2022.08.15 |
| 군집화 (0) | 2022.08.01 |
| KNN (0) | 2022.07.29 |
| 의사결정나무 (0) | 2022.07.25 |
