SVM(Support Vector Machine)
사용하기 편리하면서 높은 정확도를 보이는 지도학습 알고리즘
결정경계선(decision boundary)를 지정
결정경계: 서로 다른 분류값을 결정하는 경계
N: 데이터의 벡터 공간
결정 경계=N-1차원
그래서 때로는 결정 경계를 초평면(hyperplane)이라고 하기도 함
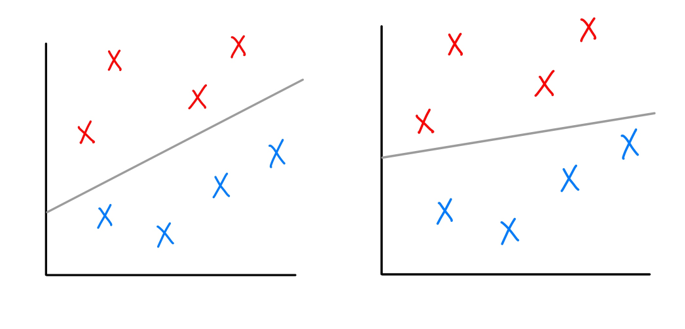
결정경계선이 데이터포인트에 가까이 위치할수록 조금의 속성 차이에도 분류값이 달라질 수 있어 예측의 정확도가 불안정해짐
Support vector: 결정 경계선을 찾는데 사용되는 개념
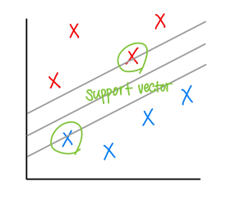
Vector: 2차원 공간 상에 나타난 데이터 포인트
Support vector: 결정 경계선과 가장 가까이 맞닿은 데이터 포인트
마진(margin): 서포트 벡터와 결정 경계 사이의 거리
SVM의 목표는 마진을 최대로 하는 결정 경계를 찾는 것
→ 새로운 데이터에 대해 안정적으로 분류하기 위해서
비용(cost)
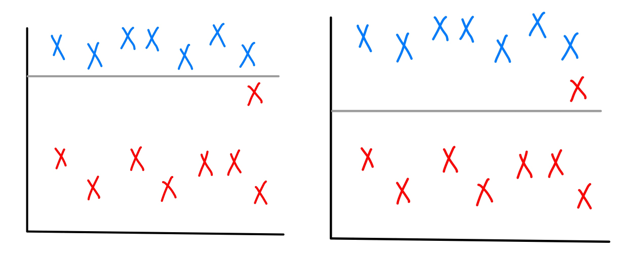
(왼쪽보다 오른쪽이 훨씬 합리적임)
약간의 오류를 허용하기 위해 비용 변수 사용
비용이 낮으면, 마진이 높고 학습 에러율을 증가시키는 방향으로 결정 경계선 만들어짐!
비용이 높으면, 마진이 낮고 학습 에러율을 감소시키는 방향으로 결정 경계선 만들어짐!
비용이 낮으면, 과소적합의 위험
비용이 높으면, 과대적합의 위험
커널 트릭
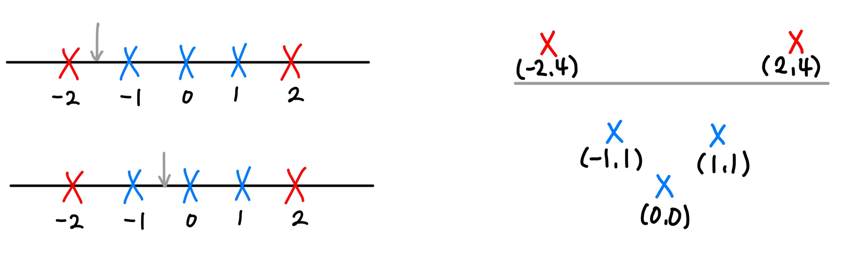
1차원의 결정경계는 0차원으로 나타내야 하므로 점 하나로 구분해야 한다. 하지만 점 하나로 완벽히 구분할 수 있는 위치는 존재하지 않는다.
N-1차원의 초평면으로 두 데이터 집단을 구분해야 하는 SVM의 입장에서 문제, 그래서 주어진 저차원 벡터 공간의 데이터를 고차원 벡터 공간으로 옮겨주어서 결정 경계를 찾는 방법을 고안
이때 저차원 데이터를 고차원 데이터로 옮겨주는 함수를 매핑 함수라고 함
ex) 1차원 데이터를 2차원으로 옮겨주는 경우, y=x2의함수를 이용하면 완벽히 분류하는 결정경계선을 만들 수 있음
하지만 매핑 함수를 가지고 실제로 많은 양의 데이터를 저차원에서 고차원으로 옮기는 것은 너무 많은 계산량을 요구함
그래서 실제로 데이터를 고차원으로 보내지 않지만 동일한 효과를 줘서 빠른 속도로 결정경계선을 만드는 방법인 커널 트릭(kernel trick)사용
SVM이 2차원 벡터 공간 상에서 직선이 아닌 결정 경계선으로 데이터를 분류한 경우 모두 커널 트릭의 결과임
- 선형 SVM: 커널을 사용하지 않고 데이터를 분류, 비용을 조절해서 마진의 크기 조절가능
- 커널 트릭: 선형 분리가 주어진 차원에서 불가능할 경우 고차원으로 데이터를 옮기는 효과를 통해 결정 경계를 찾음
비용과 gamma를 조절해서 마진을 조절 가능
커널 기법 중 일반적으로 가우시안 RBF 커널이 사용됨
가우시안 RBF
데이터포인트에 적용되는 가우시안 함수의 표준편차를 조정하여 결정 경계의 곡률을 결정
여기서 표준편차 조정 변수를 감마(gamma)라고 함
감마가 커지면 데이터포인트별로 허용하는 표준편차가 작아져서 결정 경계가 작아지면서 구부러짐
파라미터 튜닝
- 비용: 마진 너비 조절 변수, 클수록 마진 너비가 좁아지고, 작을수록 마진 너비가 넓어짐
- 감마: 커널의 표준 편차 조절 변수, 작을수록 데이터포인트의 영향이 커져서 경계가 완만해지고, 클수록 데이터포인트가 결정 경계에 영향을 적게 미쳐 경계가 구부러짐
장점
- 커널 트릭을 사용함으로써 특성이 다양한 데이터를 분류하는데 강함
- 파라미터를 조정해서 과대적합 및 과소적합에 대처 가능
- 적은 학습 데이터로도 딥러닝만큼 정확도가 높은 분류 기대 가능
단점
- 데이터 전처리 과정이 중요
- 특성이 많은 경우 결정 경계 및 데이터의 시각화가 어려움
SVM - IRIS dataset
https://github.com/ornni/ML_algorithm/blob/main/SVM/SVM_code_IRIS.md
SVM(OvR, OvO) - MNIST dataset
https://github.com/ornni/ML_algorithm/blob/main/SVM/multi_class_code(OvR%2COvO)_MNIST.md
'AI&ML > ML algorithms' 카테고리의 다른 글
| Naive Bayes (0) | 2022.08.15 |
|---|---|
| 군집화 (0) | 2022.08.01 |
| KNN (0) | 2022.07.29 |
| 의사결정나무 (0) | 2022.07.25 |
| 선형 회귀 (0) | 2022.07.18 |

